The probability current (density) is defined in the 1D case as
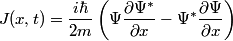 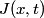 represents the rate at which probability is ``flowing" past the point represents the rate at which probability is ``flowing" past the point  . We plug in the given formula for . We plug in the given formula for 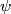 to find that to find that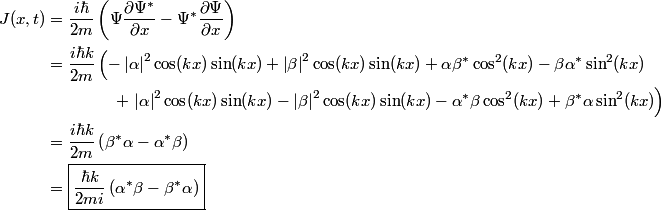 Therefore, answer (E) is correct. |
The probability current (density) is defined in the 1D case as
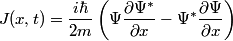 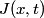 represents the rate at which probability is ``flowing" past the point represents the rate at which probability is ``flowing" past the point  . We plug in the given formula for . We plug in the given formula for 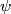 to find that to find that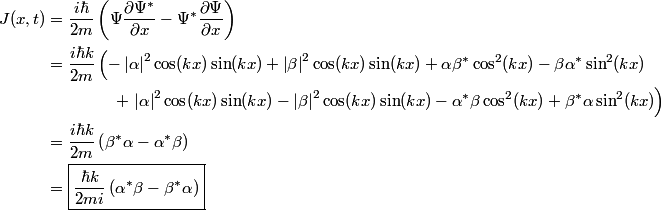 Therefore, answer (E) is correct. |